普林斯顿算法课程Part1-week5

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

平衡搜索树

2-3树

之前已经学习过了符号表的一些实现，不过我们的目标是将增删查的效率降为 logN。

2-3树为了保证平衡性，规定每个节点可以存储1或2个值，存储1个值的节点分两个子节点，存储2个值得节点分三个子节点。且节点间的大小关系如下图所示。

1

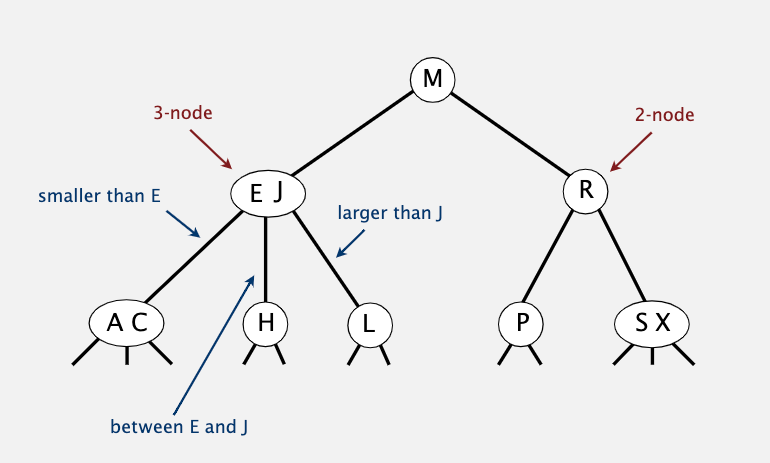
比较有意思的是它的插入过程。比如在上图的树中插入元素 Z，我们可以一直对比到最右下角的 S/X 节点，将 Z 插入该节点，这样它就变成了一个四分支节点。然后进行节点分裂，X 与父节点 R 组合在一起，S 和 Z 节点分离生成两个新节点。

2

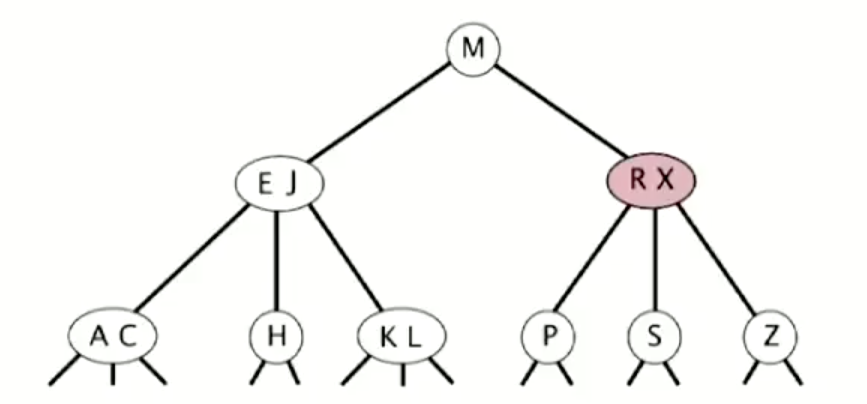
因为 2-3 树的平衡性很好，所以增删改查等操作仅仅需要 clgN 的时间复杂度。不过它太过复杂，需要考虑很多这种情况，所以并没有给出具体实现代码。我们有更好的解决方案。

红黑树

听到这几个字心情非常激动，大名鼎鼎的红黑树，无论是工作面试还是读研考试都会涉及到，而我一直畏惧没有接触。

在开讲前老爷子说了这么一番话：

On a personal note, I wrote a research paper on this topic in 1979 with Leo Givas and we thought we pretty well understood these data structures at that time and people around the world use them in implementing various different systems. But just a few years ago for this course I found a much simpler implementation of red-black trees and this is just the a case study showing that there are simple algorithms still out there waiting to be discovered and this is one of them that we’re going to talk about.

没想到屏幕后的教授就是红黑树的作者之一，并且在准备这门课时又想出了一种更简单的实现方法。能有幸听到红黑树作者讲红黑树，这是一件多么幸福的事啊。

其实红黑树就是对 2-3 树的一种更简单的实现。即含有两个键值的节点，将较小的节点分为较大节点的左子树，两者连接部分用红色标记。

3

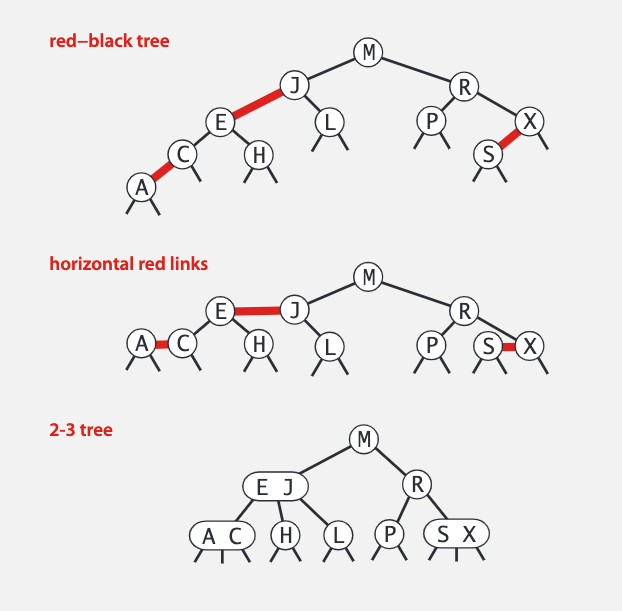
红黑树的 get()、floor() 等方法的实现跟普通的 BST 一样，只不过因为红黑树具有更好的平衡性，实际的操作速度会更快，在这里不进行详细的实现。

下面是红黑树的私有成员，主要多了标记红黑的部分。

4

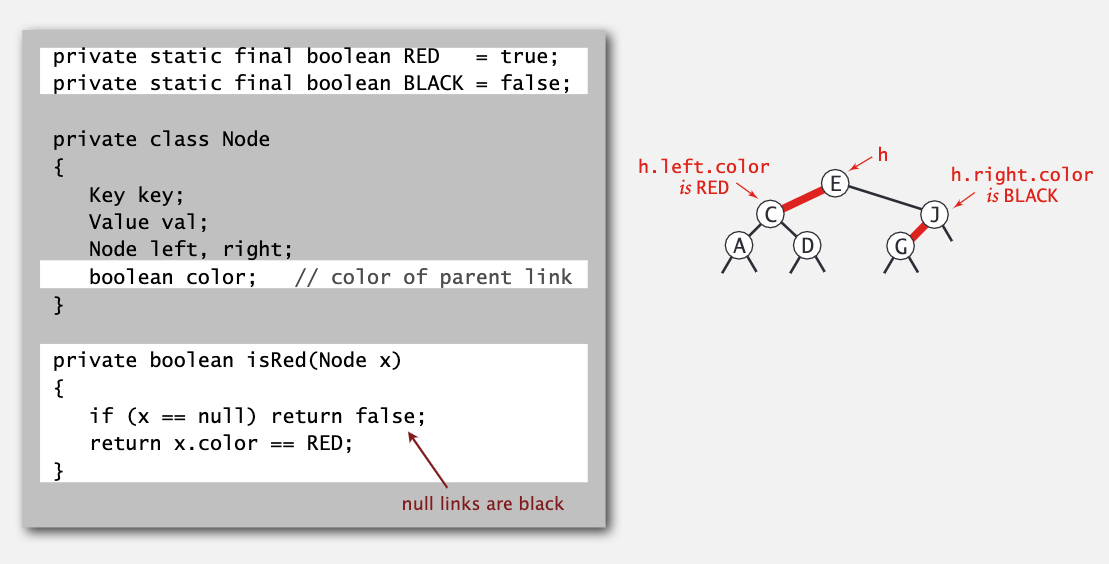
我们还需要实现一些私有类，便于插入删除等操作的实现。

1
2
3
4
5
6
7
8
private Node rotateLeft(Node h) {
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    x.color = h.color;
    h.color = RED;
    return x;
}

有的时候红黑树会产生错误，即红色端链接在父节点的右分支上。上面的操作可以将子节点移动到左分支上。

1
2
3
4
5
6
7
8
private Node rotateRight(Node h) {  
    Node x = h.left;    
    h.left = x.right;   
    x.right = h;    
    x.color = h.color;    
    h.color = RED;    
    return x; 
}

在插入时，有的节点可能会产生三个键值，我们需要让子节点分裂，中间节点合并到父节点中，改变节点的颜色就可以完成这个操作。

1
2
3
4
5
private void flipColors(Node h) {
    h.color = RED;
    h.left.color = BLACK;
    h.right.color = BLACK;
}

下面就是插入元素的过程，用到了以上三种实现，就是先将元素插入到正确的位置中，再调整树的节点颜色。听老师讲的挺魔幻的，有空再好好总结一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private Node put(Node h, Key key, Value val) {
    if (h == null)
        return new Node(key, val, RED);
    if (cmp < 0)
        h.left = put(h.left, key, val);
    else if (cmp > 0)
        h.right = put(h.right, key, val);
    else 
        h.val = val;
    
    if (isRed(h.right) && !isRed(h.left))
        h = rotateLeft(h);
    if (isRed(h.left) && isRed(h.left.left))
        h = rotateRight(h);
    if (isRed(h.left) && isRed(h.right))
        flipColors(h);
        
    return h;
}

可以证明，红黑树的高度在最坏的情况下也不会超过 2lgN。

下面是红黑树的各操作的效率，很惊人了。

5

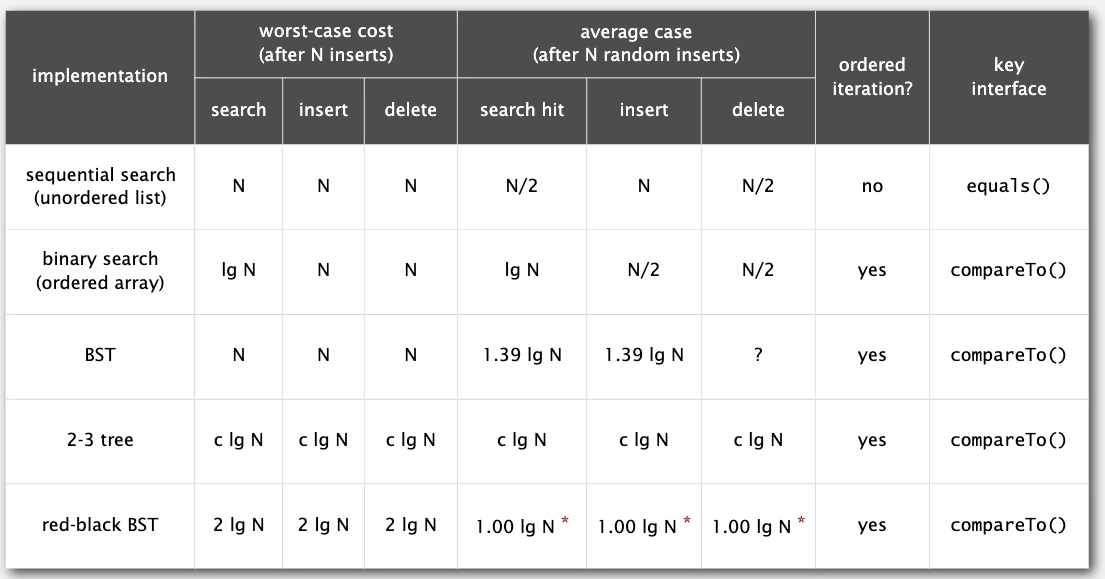
B 树

B 树是红黑树的一个实际应用。

通常我们使用外部存储来存储大量的数据，如果想计算出定位到第一页数据的时间，就需要一个切实可行的文件系统模型，B 树就可以帮我们实现这一点。

B 树的每个节点可以存储很多个键值。假设每个节点最多有 M-1 个键值，可以泛化出2-3个字树，则它只需满足以下几点：

  • 根节点至少有两个键值
  • 其他节点至少有 M/2 个键值
  • 外部节点包含 key 值
  • 内部结点包含 key 值得拷贝，以便指引查找

6

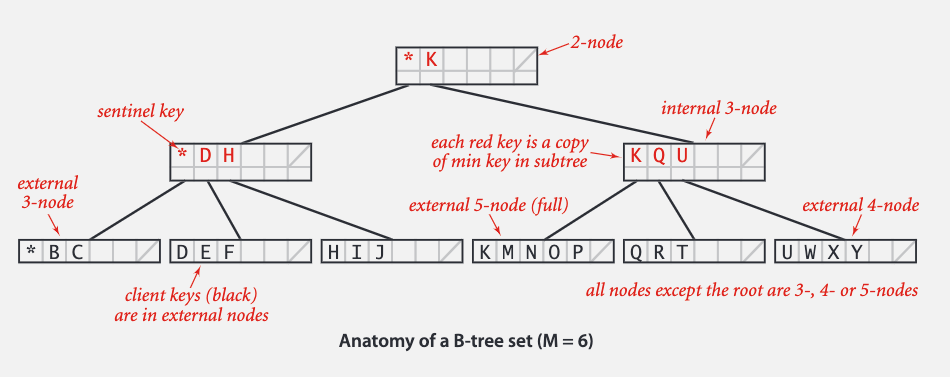
查找即依据索引一直查找到叶节点，插入也插入到叶节点需要时进行分裂。

每页 M 个键的 B 树中搜索或者插入 N 个键需要的时间在 $ \log {M-1} N $ 和 $ \log {M/2} N $ 之间。即使是万亿级别的巨型文件，我们也可以在5-6次搜索中找到任何文件。

平衡树的应用非常广泛，比如以下是红黑树的部分应用：

  • Java: java.util.TreeMap, java.util.TreeSet
  • C++ STL: map, multimap, multiset
  • Linux Kernel: completely fair scheduler, linux/rbtree.h
  • Emacs: conservative stack scanning

B 树和它的变形被广泛用于文件系统和数据库：

  • Windows: NTFS
  • Mac: HFS, HFS+
  • Linux: ReiserFS, XFS, Ext3FS, JFS
  • Databases: ORACLE, DB2, INGERS, SQL, PostgreSQL

最后老爷子讲到影视剧里也在谈论红黑树的梗，透着屏幕，你也能看得出他的骄傲和兴奋。

“A red black tree tracks every simple path from a node to a descendant leaf with the same number of black nodes.”

BST 的图形应用

一维空间搜索

它主要需要实现两个操作：

  • 区间搜索: 寻找 k1 和 k2 之间的所有键
  • 区间计数：统计 k1 和 k2 之间键的个数

这个结构通常被用于数据库的查找中。

一般用有序或者无序的数组存部分操作都会达到 N 复杂度，而显然使用普通的 BST 可以确保每个操作都是对数复杂度。就比如说下面这个区间统计的方法：

1
2
3
4
5
6
public int size(Key lo, Key hi) {
   if (contains(hi))
       return rank(hi) - rank(lo) + 1;
   else
       return rank(hi) - rank(lo);
}

下面是区间搜索的思路：

7

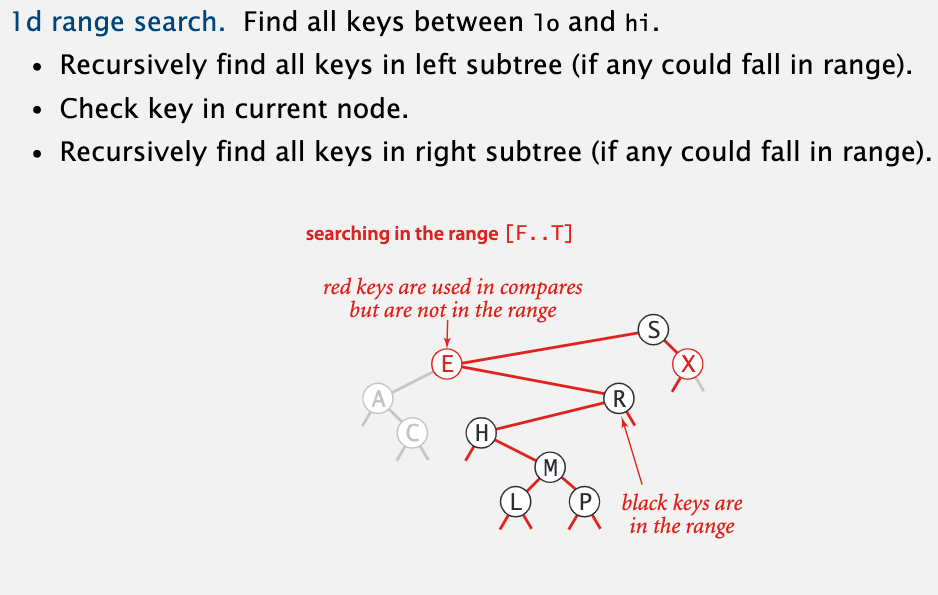
线段求交

线段相交即给出一组水平竖直的线段，求他们相交的部分。

最简单的思想是遍历每一个线段，并将它与其他线段比较，判断是否相交。不过这太慢了，会达到平方级别的复杂度，所以实际情况中根本无法使用。

我们使用扫描线算法和 BST 结合解决这个问题。假设竖直的扫描线从左到右扫描，遇到点就把它加到 BST 中，并记录 y 坐标，再次遇到这个 y 坐标的点就证明该条线段已经扫描成功，就把它移除 BST。

8

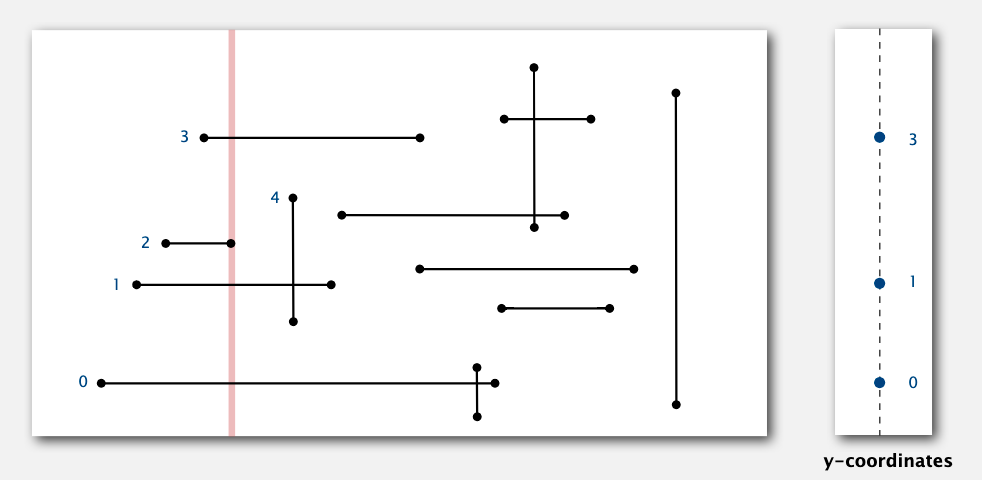
如果遇到竖直的线，就使用一维空间搜索看两个端点之间有没有水平直线的点，如果有，则证明他们相交。

9

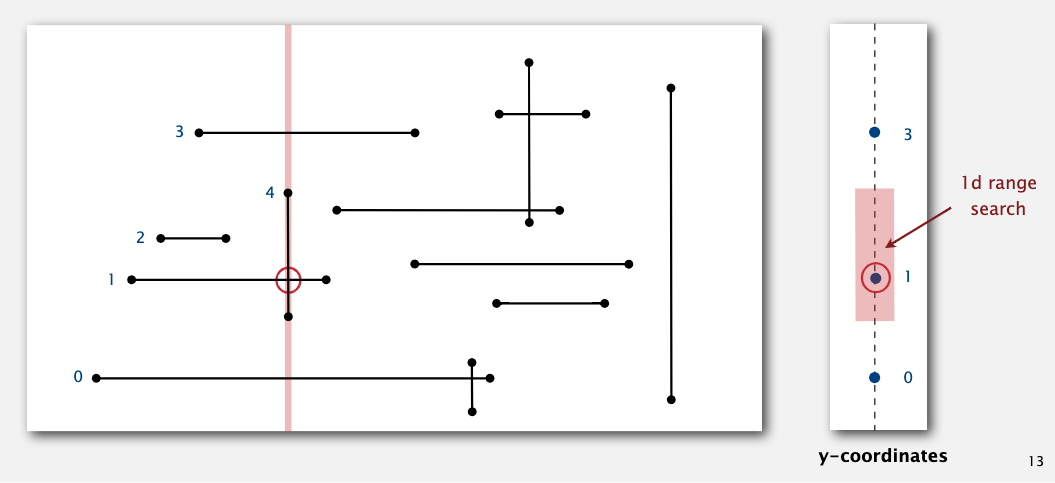
这个算法的复杂度就降到了 NlogN。

K 维树

其中一个应用是统计二维平面中的点。通常情况下，二维平面中的点分布不均匀，所以采用递归分割的方式分割平面。

下面这张图清楚地表明了该 2d 树的数据结构，它的搜索效率一般只需 R + logN，最差为 R + √N。

10

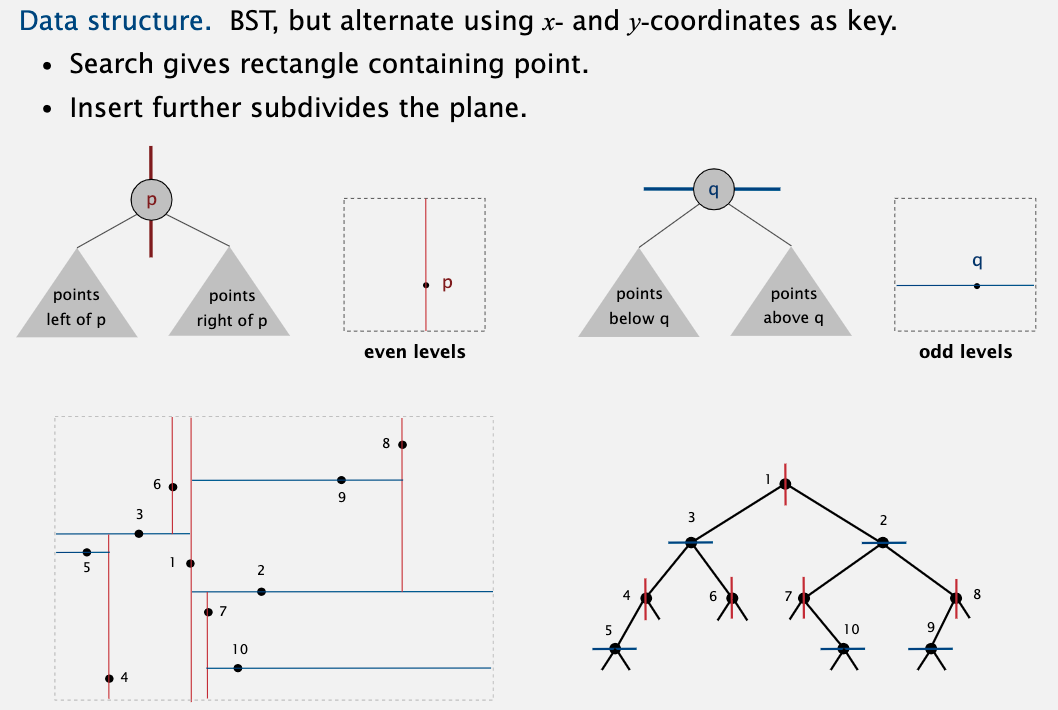
还有一个应用是寻找与某个点距离最近的点。其实道理也很类似，就是将平面分区域搜索。

还有集群模拟、N 体问题等都有提到，不得不说这门课与前沿科技的结合还是非常密切的。

区间搜索树和矩形相交

这两点其实和线段相交类似，区间搜索树即每个节点的键值变为区间，实际上还是用 BST 做存储；矩形相交也用的扫描线，遇到竖直的矩形时用区间搜索看两端点之间是否含有子区间，如果有，则相交。

这部分没有特别细致的看，大概有个印象就是 BST 的应用的时间复杂度差不多都是对数级别。

编程作业：Kd 树

本周的作业就是实现 API，二维空间内给定一些点，可以判断点是否在给定区域内或者离一个点最近的点是哪个，有点类似 KNN 的算法。

12

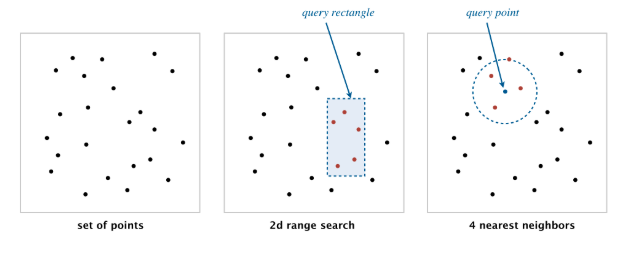
第一种方法是用红黑树实现的，其实就是调用已有的数据结构实现 API，两个算法都用的暴力方法，感觉是想让学生熟悉一下整个 API，或是为了对之后高效的实现进行对比。

点击显/隐内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
public class PointSET {

    private SET<Point2D> set;

    private static final double RADIUS = 0.01;

    /**
     * construct an empty set of points
     */
    public PointSET() {
        this.set = new SET<>();
    }

    /**
     * is the set empty?
     * @return
     */
    public boolean isEmpty() {
        return set.size() == 0;
    }

    /**
     * number of points in the set
     * @return
     */
    public int size() {
        return set.size();
    }

    /**
     * add the point to the set (if it is not already in the set)
     * @param p
     */
    public void insert(Point2D p) {
        if (p == null)
            throw new IllegalArgumentException();
        set.add(p);
    }

    /**
     * does the set contain point p?
     * @param p
     * @return
     */
    public boolean contains(Point2D p) {
        if (p == null)
            throw new IllegalArgumentException();
        return set.contains(p);
    }

    /**
     * draw all points to standard draw
     */
    public void draw() {
        StdDraw.setPenColor(StdDraw.BLACK);
        StdDraw.setPenRadius(RADIUS);
        for (Point2D p : set) {
            p.draw();
        }
    }

    /**
     * all points that are inside the retangle (or on the boundary)
     * @param rect
     * @return
     */
    public Iterable<Point2D> range(RectHV rect) {
        if (rect == null)
            throw new IllegalArgumentException();
        Queue<Point2D> queue = new Queue<>();
        for (Point2D p : set) {
            if (rect.contains(p))
                queue.enqueue(p);
        }
        return queue;
    }


    /**
     * a nearest neighbor in the set to point p; null if the set is empty
     * @param p
     * @return
     */
    public Point2D nearest(Point2D p) {
        if (p == null)
            throw new IllegalArgumentException();
        if (isEmpty())
            return null;
        Point2D res = set.min();
        double min = Double.POSITIVE_INFINITY;
        for (Point2D point2D : set) {
            if (p.distanceSquaredTo(point2D) < min) {
                res = p;
                min = p.distanceSquaredTo(point2D);
            }
        }
        return res;
    }
}

第二个是使用 2d 树实现，这个才是重点和难点。specification 中的描述少得可怜，就是大概说了说要实现的效果，实现方法什么的基本没提，后来在 checklist 中找到了一些思路。

一开始先实现 isEmpty() 和 size() 方法，因为它们很简单；然后实现 insert()，可以先不考虑 RectHV；再实现 contains() 后就可以写个 test 看 insert() 对不对；最后实现完 insert() 后完成 range() 和 nearest()。

点击显/隐内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
public class KdTree {

    private int count = 0;

    private Node root;

    private static class Node {
        private Point2D p;   // the point
        private RectHV rect; // the axis-aligned rectangle corresponding to this node
        private Node lb;     // the left/bottom subtree
        private Node rt;     // the right/top subtree
        private boolean isVerticle; // is the node verticle?

        public Node(Point2D p, boolean isVerticle, RectHV rect) {
            this.p = p;
            this.isVerticle = isVerticle;
            this.rect = rect;
        }
    }

    public boolean isEmpty() {
        return count == 0;
    }

    public int size() {
        return count;
    }

    public void insert(Point2D p) {
        if (p == null)
            throw new IllegalArgumentException();
        root = insert(root, p, null, 0);
    }

    private Node insert(Node n, Point2D p, Node pre, int direction) {
        if (n == null) {
            count++;
            if (direction == 0)
                return new Node(p, true, new RectHV(0, 0, 1, 1));

            RectHV preRect = pre.rect;
            if (direction == -1) {
                if (!pre.isVerticle)    // down
                    return new Node(p, true, new RectHV(pre.rect.xmin(), pre.rect.ymin(),
                                                        pre.rect.xmax(), pre.p.y()));
                else    // left
                    return new Node(p, false, new RectHV(pre.rect.xmin(), pre.rect.ymin(),
                                                        pre.p.x(), pre.rect.ymax()));
            } else if (direction == 1) {
                if (!pre.isVerticle)    // up
                    return new Node(p, true, new RectHV(pre.rect.xmin(), pre.p.y(),
                                                        pre.rect.xmax(), pre.rect.ymax()));
                else    // right
                    return new Node(p, false, new RectHV(pre.p.x(), pre.rect.ymin(),
                                                         pre.rect.xmax(), pre.rect.ymax()));
            }
        } else {
            int cmp = 0;
            if (n.isVerticle)
                cmp = p.x() < n.p.x() ? -1 : 1;
            else
                cmp = p.y() < n.p.y() ? -1 : 1;
            // 去重
            if (p.equals(n.p))
                cmp = 0;

            if (cmp == -1)
                n.lb = insert(n.lb, p, n, cmp);
            else if (cmp == 1)
                n.rt = insert(n.rt, p, n, cmp);
        }

        return n;
    }


    public boolean contains(Point2D p) {
        Node current = root;
        while (current != null) {
            if (current.p.compareTo(p) == 0)
                return true;
            else if (current.isVerticle) {
                // x
                if (p.x() < current.p.x())
                    current = current.lb;
                else
                    current = current.rt;
            } else {
                // y
                if (p.y() < current.p.y())
                    current = current.lb;
                else
                    current = current.rt;
            }
        }
        return false;
    }

    public Iterable<Point2D> range(RectHV rect) {
        if (rect == null)
            throw new IllegalArgumentException();
        Queue<Point2D> queue = new Queue<>();
        range(rect, root, queue);
        return queue;
    }

    private void range(RectHV rect, Node x, Queue<Point2D> queue) {
        if (x == null)
            return;
        if (rect.contains(x.p))
            queue.enqueue(x.p);
        if (x.lb != null && x.lb.rect.intersects(rect))
            range(rect, x.lb, queue);
        if (x.rt != null && x.rt.rect.intersects(rect))
            range(rect, x.rt, queue);
    }


    public Point2D nearest(Point2D p) {
        if (p == null)
            throw new IllegalArgumentException();
        if (root == null)
            return null;
        return nearest(p, root, root.p);
    }

    private Point2D nearest(Point2D goal, Node x, Point2D nearest) {
        if (x == null)
            return nearest;

        if (goal.distanceSquaredTo(x.p) < goal.distanceSquaredTo(nearest))
            nearest = x.p;

        int cmp = 0;
        if (x.isVerticle)
            cmp = goal.x() < x.p.x() ? -1 : 1;
        else
            cmp = goal.y() < x.p.y() ? -1 : 1;
        if (x.p.equals(goal))
            cmp = 0;

        if (cmp == -1) {
            nearest =  nearest(goal, x.lb, nearest);
            if (x.rt != null && x.rt.rect.distanceSquaredTo(goal) < nearest.distanceSquaredTo(goal))
                nearest = nearest(goal, x.rt, nearest);
        } else if (cmp == 1) {
            nearest =  nearest(goal, x.rt, nearest);
            if (x.lb != null && x.lb.rect.distanceSquaredTo(goal) < nearest.distanceSquaredTo(goal))
                nearest = nearest(goal, x.lb, nearest);
        }

        return nearest;
    }

    public void draw()
    {
        draw(root);
    }

    private void draw(Node x)
    {
        if (x == null) return;
        draw(x.lb);
        draw(x.rt);
        StdDraw.setPenColor(StdDraw.BLACK);
        StdDraw.setPenRadius(0.01);
        x.p.draw();
        StdDraw.setPenRadius();
        // draw the splitting line segment
        if (x.isVerticle)
        {
            StdDraw.setPenColor(StdDraw.RED);
            StdDraw.line(x.p.x(), x.rect.ymin(), x.p.x(), x.rect.ymax());
        }
        else
        {
            StdDraw.setPenColor(StdDraw.BLUE);
            StdDraw.line(x.rect.xmin(), x.p.y(), x.rect.xmax(), x.p.y());
        }
    }
}

其实最后总结起来几句话就完了，coding 的过程中真的问题百出。2d 树的建立就有很多问题，比如不知道怎样区别树的比较方向、RectHV 有什么用等；到 range() 和 nearest() 方法时也比较麻烦，比较那部分一点疏忽就跑不出来结果。

不过做了这么多次 programming assignment 也熟悉了，不停改不停翻 specification 和 checklist 总会写出来的，实在不行就看别人写的博客。

11

-------------本文结束感谢您的阅读-------------

本文标题:普林斯顿算法课程Part1-week5

文章作者:DianGe Du

发布时间:2019年04月28日 - 17:13

最后更新:2019年06月07日 - 14:40

原始链接:https://dudg1021.github.io/2019/04/28/普林斯顿算法课程Part1-week5.html

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。