普林斯顿算法课程Part1-week4

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

优先队列和符号表

优先队列在入队时与传统队列相同，而出队时可以指定规则，比如最大元素/最小元素出队等，下面是一个简单的 API：

1

二叉堆

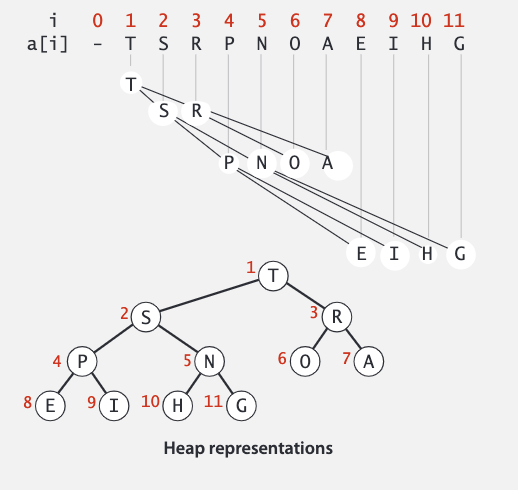
二叉堆是堆有序的完全二叉树，键值存储在节点上，且父元素的键值比子元素的键值大。我们可以推测出最大的键值在根节点上，也就是 a[1]（不使用数组的第一个位置）。

二叉堆实际存储在数组中，如果一个节点的索引是 k，那么它的父节点的索引是 k / 2， 子节点的索引是 2k 和 2k + 1。

2

如果某一节点的堆有序被破坏了（子节点比父节点大），我们可以使用下面的算法恢复：

1
2
3
4
5
6
private void swim(int k) {
    while (k > 1 && less(k / 2, k)) {
        exch(k, k / 2);
        k = k / 2;
    }
}

因此实现添加操作时将待添加的元素插入到树的下一个子节点，然后通过 swim() 方法将其移动到正确的位置上，这个操作最多需要 1 + lgN 次比较。

1
2
3
4
public void insert(Key x) {
    pq[++N] = x;
    swim(N);
}

还有一种情况是父节点比两个子节点小，使用“下沉”的思想可以很好解决它：

1
2
3
4
5
6
7
8
9
10
11
private void sink(int k) {
    while (2 * k <= N) {
        int j = 2 * k;
        if (j < N && less(j, j + 1))
            j++;
        if (!less(k, j))
            break;
        exch(k, j);
        k = j;
    }
}

sink() 方法利于实现删除操作，将首节点和尾节点互换位置，删除尾节点，再将首节点移动到合适的位置。这个操作最多需要 2lgN 次比较。

1
2
3
4
5
6
7
public Key delMax() {
    Key max = pq[1];
    exch(1, N--);
    sink(1);
    pq[N + 1] = null;
    return max;
}

下面是完整的二叉堆的实现，这种实现的插入和删除操作都是 logN 的时间复杂度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class MaxPQ<Key extends Comparable<Key>> {
    private Key[] pq;
    private int N;
    
    public MaxPQ(int capacity) {
        pq = (Key[]) new Comparable[capacity + 1];
    }
    
    public boolean isEmpty() {
        return N == 0;
    }
    
    public void insert(Key key)
    public Key delMax()
    private void swim(int k)
    private void sink(int k)
    
    private boolean less(int i, int j) {
        return pq[i].compareTo(pq[j]) < 0;
    }
    
    private void exch(int i, int j) {
        Key t = pq[i];
        pq[i] = pq[j];
        pq[j] = t;
    }
}

堆排序

堆排序分为两个阶段，第一个阶段是将数组安排到一个堆中，最好的方法是使用“下沉”操作，N 个元素只需要少于 2N 次比较和少于 N 次交换。

第二个阶段是通过二叉堆的删除方法，每次将二叉堆中最大的元素筛选出来，筛选出来的数组则是有序的。

1
2
3
4
5
6
7
8
9
10
11
12
public class Heap {
    public static void sort(Comparable[] pq) {
        int N = pq.length;
        for (int k = N / 2; k >= 1; k--)
            sink(a, k, N);
        while (N > 1) {
            exch(a, 1, N--);
            sink(a, 1, N);
        }
    }
    ...
}

堆排序最多需要 2NlgN 次比较和交换操作，而且它是一个原地算法。

不过堆排序并不像想象中那么好，比如 Java 的 sort() 方法中就没有使用堆排序，它主要由以下三个缺点：

  • 内循环太长
  • 没能很好地利用缓存
  • 不稳定

关于第二点，我一开始也不是很理解，后来 Google 除了答案。堆排序的过程中经常访问相距很远的元素，不利于缓存发挥作用；而快排等算法只会访问到局部的数据，因此缓存能更大概率命中，即局部性更强。

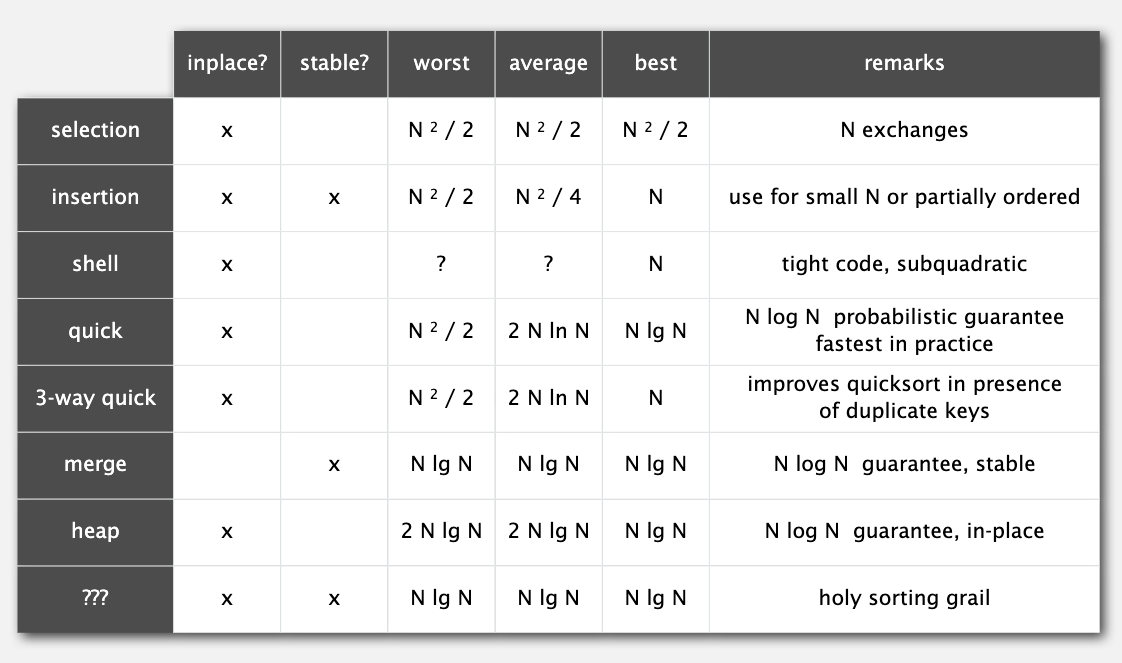
下面是截至目前所学排序算法的总结：

3

符号表

下面是符号表的 API。

6

位查找

实现符号表最简单的方法是使用链表，不过插入和查找操作都需要遍历整个链表，复杂度为 N。

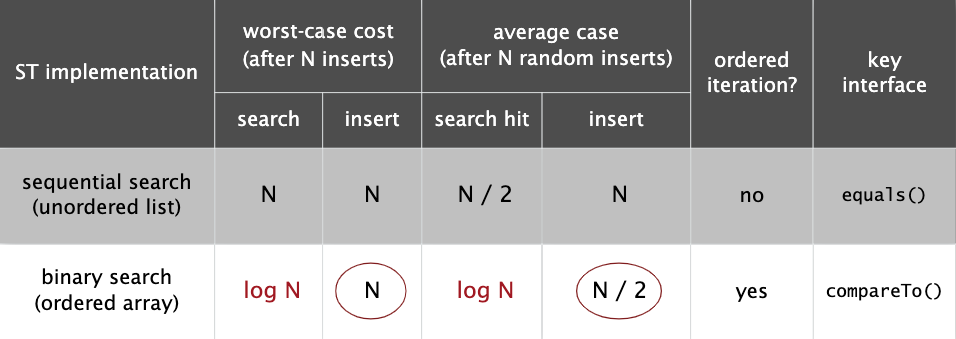
因此我们可以使用两个数组实现，一个存储 key，一个存储 value，且存储是有序的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public Value get(Key key) {
    if (isEmpty())
        return null;
    int i = rank(key);
    if (i < N && keys[i].compareTo(key) == 0)
        return vals[i];
    else 
        return null;
}
private int rank(Key key) {
    int lo = 0, hi = N - 1;
    while (lo <= hi) {
        int mid = lo + (hi - lo) / 2;
        int cmp = key.compareTo(keys[mid]);
        if (cmp < 0)
            hi = mid - 1;
        else if (cmp > 0)
            lo = mid + 1;
        else 
            return mid;
    }
    return lo;
}

不过插入要移动数组元素。

7

二分查找树

二分查找树实际上是一颗二叉树，节点上有值。父节点比所有左子节点上的元素大，比所有右子节点上的元素小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
public class BST<Key extends Comparable<Key>, Value> {
    private Node root;
    
    private class Node {
        private Key key;
        private Value val;
        private Node left, right;
        private int count;
        public Node(Key key, Value val) {
            this.key = key;
            this.value = value;
        }
    }
    
    public void put(Key key, Value val) {
        root = put(root, key, val);
    }
    
    private Node put(Node x, Key key, Value val) {
        if (x == null)
            return new Node(key, val);
        int cmp = key.compareTo(x.key);
        if (cmp < 0)
            x.left = put(x.left, key, val);
        else if (cmp > 0)
            x.right = put(x.right, key, val);
        else
            x.val = val;
        x.count = 1 + size(x.left) + size(x.right);
        return x;
    }
    
    public Value get(Key key) {
        Node x = root;
        while (x != null) {
            int cmp = key.compareTo(x.key);
            if (cmp < 0)
                x = x.left;
            else if (cmp > 0)
                x = x.right;
            else
                return x.val;
        }
        return null;
    }
    
    public int size() {
        return size(root);
    }
    
    private int size(Node x) {
        if (x == null)
            return 0;
        return x.count;
    }
    
    public Key min() {
        return min(root).key;
    }
    
    private Node min(Node x) {
        if (x.left == null)
            return x;
        return min(x.left);
    }
    
    public Key floor(Key key) {
        Node x = floor(root, key);
        if (x == null)
            return null;
        return x.key;
    }
    
    private Node floor(Node x, Key key) {
        if (x == null)
            return null;
        int cmp = key.compareTo(x.key);
        if (cmp == 0)
            return x;
        if (cmp < 0)
            return floor(x.left, key);
        Node t = floor(x.right, key);
        if (t != null)
            return t;
        else
            return x;
    }
    
    /** How many keys < k */
    public int rank(Key key) {
        return rank(key, root);
    }
    
    private int rank(Key key, Node x) {
        if (x == null)
            return 0;
        int cmp = key.compareTo(x.key);
        if (cmp < 0)
            return rank(key, x.left);
        else if (cmp > 0)
            return 1 + size(x.left) + rank(key, x.right);
        else 
            return rank(x.left); 
    }
    
    public Iterator<Key> keys() {
        Queue<Key> q = new Queue<>();
        inorder(root, q);
        return q;
    }
    
    private void inorder(Node x, Queue<Key> q) {
        if (x == null)
            return;
        inorder(x.left, q);
        q.enqueue(x.key);
        inorder(x.right, q);
    }
    
    public void deleteMin() {
        root = deleteMin(root);
    }
    
    private Node deleteMin(Node x) {
        if (x.left == null)
            return x.right;
        x.left = deleteMin(x.left);
        x.count = 1 + size(x.left) + size(x.right);
        return x;
    }
    
    public void delete(Key key) {
        root = delete(root, key);
    }
    
    private Node delete(Node x, Key key) {
        if (x == null) 
            return null;
        int cmp = key.compareTo(x.key);
        if (cmp < 0)
            x.left = delete(x.left, key);
        else if (cmp > 0)
            x.right = delete(x.right, key);
        else {
            if (x.right == null)
                return x.left;
            if (x.left == null)
                return x.right;
            
            Node t = x;
            x = min(t.right);
            x.right = deleteMin(t.right);
            x.left = t.left;
        }
        x.count = size(x.left) + size(x.right) + 2;
        return x;
    }
}

BST 的效率跟插入元素的顺序有关，最差的情况是所有节点都在其父节点的右子树上。

下面是二叉查找树各方法的效率：

8

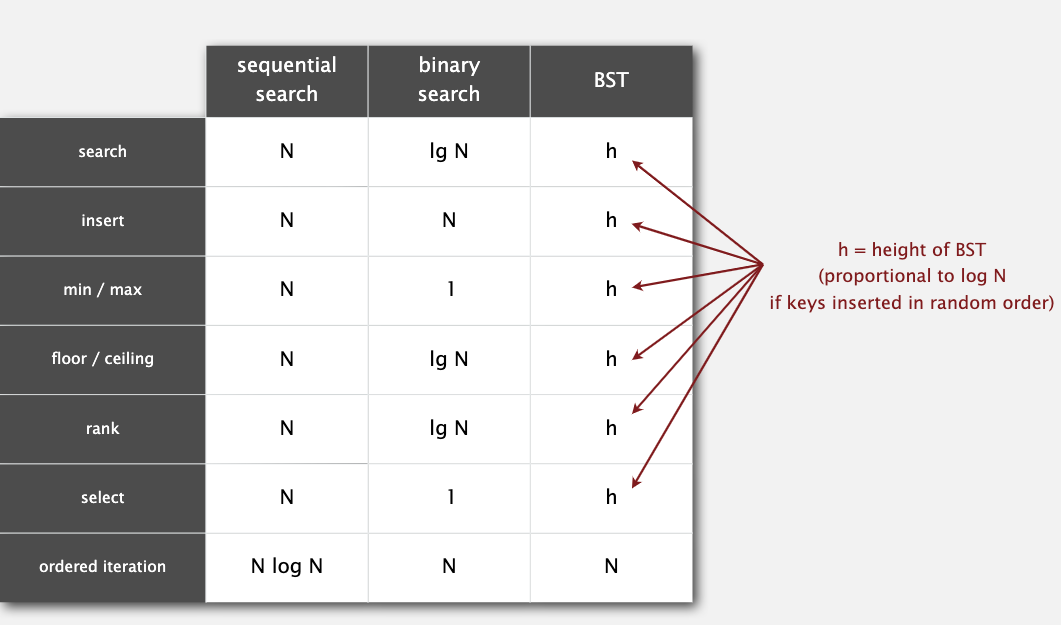
下面是二叉查找树与之前数据结构的对比:

9

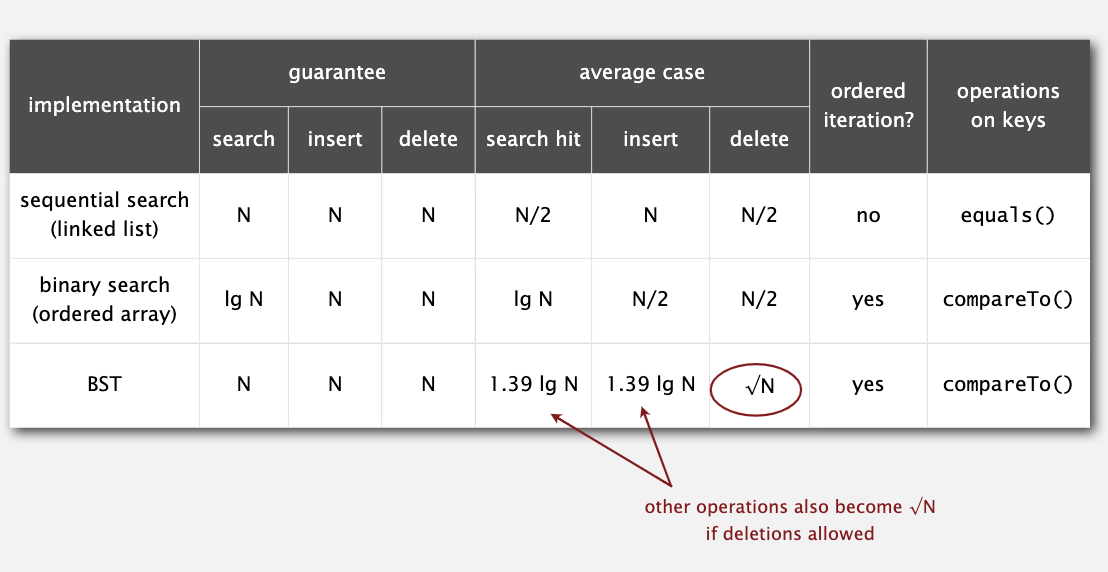
它的删除算法不算好，树的形状很容易偏向一侧，至今都没有什么好的解决办法。

编程作业：8 Puzzle

本次的作业是写一个游戏 AI，游戏即将一个无序的矩阵通过空白格的交换达到有序，如下图所示：

1
2
3
4
5
   1  3        1     3        1  2  3        1  2  3        1  2  3
4  2  5   =>   4  2  5   =>   4     5   =>   4  5      =>   4  5  6
7  8  6        7  8  6        7  8  6        7  8  6        7  8 

initial        1 left          2 up          5 left          goal

讲真这次的作业做了好久好久，主要是不理解一开始给出的算法，只能硬着头皮边实现 API 边理解文档，最后调 bug 又调了两个小时，总之感觉是目前接触到最难得一次吧。

解决整个问题最核心的是 A* search 算法。每个矩阵都看作是一个搜索节点，一开始在 MinPQ 中插入所给的节点，然后删除最小的节点，并将最小节点的所有移动方法再插入到优先队列中，重复上述操作，直到队列中的最小节点有序。

所谓最小，即整个矩阵的复杂度最小，有 Hamming 和 Manhattan 两种优先度算法。两种方法都要经过测试，不过真正实现的时候要用 Manhattan 算法。

A* search 算法的操作可以想象成一棵博弈树，为了最终找到操作的过程，每个子节点还要存有父节点的引用。

4

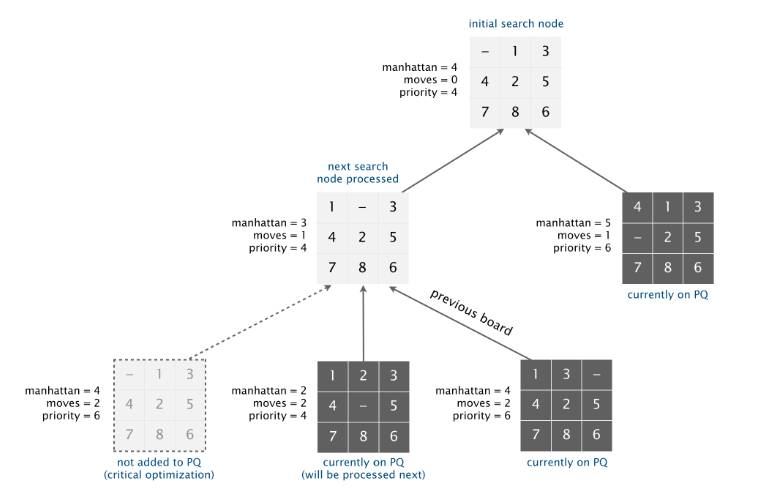
还要考虑的一种情况是，所给的矩阵根本无法调整为有序。这里的算法一直都不是很懂，一开始将原始节点的两个位置互换创建伴随节点啊，然后进行和原始节点相同的操作，如果原始节点无解的话，那么伴随节点一定有解。有兴趣的可以看一下这篇论文，给出了算法的证明。

大致梳理了一下思路后，就没有什么难懂的地方了。

Board 类主要就是记录输入数据，并实现比较规则以及一些生成方法供后续使用。

点击显/隐内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
public class Board {

    private final char[] blocks;
    private final int n;
    private int blankPos;

    /**
     * construct a board from an n-by-n array of blocks
     * @param blocks
     */
    public Board(int[][] blocks) {
        if (blocks == null || blocks[0] == null)
            throw new NullPointerException();
        this.n = blocks.length;
        this.blocks = new char[n * n + 1];
        // 二维转一维
        int index = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                this.blocks[++index] = (char) blocks[i][j];
                if (this.blocks[index] == 0)
                    this.blankPos = index;
            }
        }
    }


    /**
     * board dimension n
     * @return
     */
    public int dimension() {
        return this.n;
    }

    /**
     * number of blocks out of place
     * @return
     */
    public int hamming() {
        int count = 0, index = 0;
        for (int i = 1; i < blocks.length; i++) {
            index++;
            if (blocks[index] != i && blocks[index] != 0)
                count++;
        }
        return count;
    }

    /**
     * sum of Manhattan distancces between blocks and goal
     * @return
     */
    public int manhattan() {
        int count = 0, index = 0;
        for (int k = 1; k < blocks.length; k++) {
            int value = blocks[++index];
            if (value != 0) {
                int correctPositionX = value % n == 0 ? value / n : value / n + 1,
                        correctPositionY = (value % n == 0 ? n : value % n);
                int currentPositionX = index % n == 0 ? index / n : index / n + 1,
                        currentPositionY = (index % n == 0 ? n : index % n);
                count += Math.abs(correctPositionX - currentPositionX) +
                        Math.abs(correctPositionY - currentPositionY);
                // System.out.println(
                //         "current:(" + currentPositionX + ", " + currentPositionY + ")" +
                //         "\tcorrect:(" + correctPositionX + ", " + correctPositionY + ")" +
                //         "\tvalue: "+ value + "\tcount: " + count
                // );
            }
        }
        return count;
    }

    /**
     * is this board the goal board?
     * @return
     */
    public boolean isGoal() {
        for (int i = 1; i < blocks.length - 2; i++)
            if (blocks[i] > blocks[i + 1])
                return false;
        return true;
    }

    /**
     * a board that is obtained by exchanging any pair of blocks
     * @return
     */
    public Board twin() {
        int index1 = -1, index2 = -1;
        if (blocks[1] != 0 && blocks[2] != 0) {
            index1 = 1;
            index2 = 2;
        } else {
            index1 = n + 1;
            index2 = n + 2;
        }
        return new Board(exchangeTwoEle(index1, index2));
    }

    /**
     * exchange two elements and transfer to int[][]
     * @param index1
     * @param index2
     * @return
     */
    private int[][] exchangeTwoEle(int index1, int index2) {
        int[][] bs = new int[n][n];
        int value1 = blocks[index1], value2 = blocks[index2];
        int index = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                index++;
                if (index == index1)
                    bs[i][j] = value2;
                else if (index == index2)
                    bs[i][j] = value1;
                else
                    bs[i][j] = blocks[index];
            }
        }
        return bs;
    }

    /**
     * does this board equal y?
     * @param y
     * @return
     */
    public boolean equals(Object y) {
        if (this == y)
            return true;
        if (y == null)
            return false;
        if (this.getClass() != y.getClass())
            return false;
        Board b = (Board) y;
        if (!Arrays.equals(this.blocks, b.blocks))
            return false;
        if (this.n != b.n)
            return false;
        return true;

    }

    /**
     * all neighboring boards
     * @return
     */
    public Iterable<Board> neighbors() {
        Stack<Board> stack = new Stack<>();
        int index = blankPos;
        if (index > n) {
            // up
            stack.push(new Board(exchangeTwoEle(index, index - n)));
        }
        if (index + n <= n * n) {
            // down
            stack.push(new Board(exchangeTwoEle(index, index + n)));
        }
        if (index > 0 && (index - 1) % n != 0) {
            // left
            stack.push(new Board(exchangeTwoEle(index, index - 1)));
        }
        if (index < n * n && (index + 1) % n != 1) {
            // right
            stack.push(new Board(exchangeTwoEle(index, index + 1)));
        }

        return stack;
    }

    /**
     * string representation of this board (in the output format sprcified below)
     * @return
     */
    public String toString() {
        StringBuilder sb = new StringBuilder();
        sb.append(n + "\n");
        for (int i = 1; i <= n * n; i++) {
            sb.append(String.format("%2d ", (int) blocks[i]));
            if (i % n == 0)
                sb.append("\n");
        }
        return sb.toString();
    }
}

Solver 类包含一个内部类，即搜索节点，它主要包括 Board 和移动次数等信息。构造函数实现了 A* search 算法，其余方法只是为了输出结果。

点击显/隐内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
public class Solver {

    private final MinPQ<SearchNode> minPQ;
    private final MinPQ<SearchNode> twins;


    private class SearchNode implements Comparable<SearchNode> {

        private final Board board;
        private final int moves;
        private final int priority;
        private final SearchNode prevSearchNode;

        public SearchNode(Board board, int moves, SearchNode prevSearchNode) {
            this.board = board;
            this.moves = moves;
            this.priority = board.manhattan() + moves;
            this.prevSearchNode = prevSearchNode;
        }


        @Override
        public int compareTo(SearchNode sn) {
            return this.priority - sn.priority;
        }
    }


    /**
     * find a solution to the initial board (using the A* algorithm)
     * @param initial
     */
    public Solver(Board initial) {
        if (initial == null)
            throw new IllegalArgumentException();
        this.minPQ = new MinPQ<>();
        this.twins = new MinPQ<>();
        minPQ.insert(new SearchNode(initial, 0, null));
        twins.insert(new SearchNode(initial.twin(), 0, null));

        /**
         * 删最低，插相邻，重复，最后剩一个
         */
        while (!minPQ.min().board.isGoal() && !twins.min().board.isGoal()) {
            SearchNode minSearchNode = minPQ.delMin();
            SearchNode minTwins = twins.delMin();
            for (Board b : minSearchNode.board.neighbors()) {
                if (minSearchNode.moves == 0 || !b.equals(minSearchNode.prevSearchNode.board))
                    minPQ.insert(new SearchNode(b, minSearchNode.moves + 1, minSearchNode));
            }
            for (Board b : minTwins.board.neighbors()) {
                if (minTwins.moves == 0 || !b.equals(minTwins.prevSearchNode.board))
                    twins.insert(new SearchNode(b, minTwins.moves + 1, minTwins));
            }
        }
    }

    /**
     * is the initial board solvable?
     * @return
     */
    public boolean isSolvable() {
        if (minPQ.min().board.isGoal())
            return true;
        return false;
    }

    /**
     * min number of moves to solve initial board; -1 if unsolvable
     * @return
     */
    public int moves() {
        if (!isSolvable())
            return -1;
        return minPQ.min().moves;
    }

    /**
     * sequence if boards in a shortest solution; null if unsolvable
     * @return
     */
    public Iterable<Board> solution() {
        if (!isSolvable())
            return null;
        Stack<Board> stack = new Stack<>();
        SearchNode current = minPQ.min();
        while (current != null) {
            stack.push(current.board);
            current = current.prevSearchNode;
        }
        return stack;
    }
}

讲义中提到的几点优化一定要完成，效率会提高不少。还有一定要注意 Board 的输出格式，我就是少了个空格曾经一度得零分十几分。

测试数据并不是很难，我本地 puzzle50 没跑出来不过提交似乎没测试这么大的数据。可见这个 Ai 的算法还是有局限性的，对于 4*4 以上的复杂情况很难算出来。

最后部分数据超内存得了 95 分，下面上图感受一下曾经崩溃的心理。

5

幸亏不罚时。

-------------本文结束感谢您的阅读-------------

本文标题:普林斯顿算法课程Part1-week4

文章作者:DianGe Du

发布时间:2019年04月15日 - 09:31

最后更新:2019年06月07日 - 14:40

原始链接:https://dudg1021.github.io/2019/04/15/普林斯顿算法课程Part1-week4.html

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。