普林斯顿算法课程Part1-week3

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

归并排序

归并排序的思想是把数组一分为二，然后再不断将小数组递归地一分为二下去，经过一系列排序再将它们合并起来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
    for (int k = lo; k <= hi; k++)
        aux[k] = a[k];
    int i = lo, j = mid + 1;
    for (int k = lo; k <= hi; k++) {
        if (i > mid)
            a[k] = aux[j++];
        else if (j > hi)
            a[k] = aux[i++];
        else if (less(aux[j], aux[i]))
            a[k] = aux[j++];
        else
            a[k] = aux[i++];
    }
}

private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
    if (hi <= lo)
        return;
    int mid = lo + (hi - lo) / 2;
    sort(a, aux, lo, mid);
    sort(a, aux, mid+1, hi);
    if（!less(a[mid + 1], a[mid])）
        return;
    merge(a, aux, lo, mid, hi);
}

public static void sort(Comparable[] a) {
    Comparable[] aux = new Comparable[a.length];
    sort(a, aux, 0, a.length - 1);
}

归并排序可用于大量数据的排序，对于 million 和 billion 级别的数据，插入排序难以完成的任务归并排序可能几分钟就完成了。

对于 N 个元素，归并排序最多需要 NlgN 次比较和 6NlgN 次对数组的访问，并且要使用 N 个空间的辅助数组。

自底向上的归并排序

我们将归并排序的过程倒过来看，先将数组分为 2 个元素并将所有组排序，再分为 4 个元素并将所有组排序，… ，直到完成排序。

1
2
3
4
5
6
7
public static void sort(Comparable[] a) {
    int N = a.length;
    aux = new Comparable[N];
    for (int sz = 1; sz < N; sz = sz + sz) 
        for (int lo = 0; lo < N - sz; lo += sz + sz)
            merge(a, lo, lo + sz - 1, Math.min(lo+sz+sz-1, N-1));
}

这是一个完全符合工业标准的代码，除了需要额外的存储空间。时间复杂度为 O(NlogN)。

排序规则

我们可以实现 Comparator 接口来为排序算法编写不同的排序规则，以插入排序为例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static void sort(Object[] a, Comparator comparator) {
    int N = a.length;
    for (int i = 0; i < N; i++) 
        for (int j = i; j > 0 && less(comparator, a[j], a[j-1]); j--)
            exch(a, j, j - 1);
}

private static boolean less(Comparator c, Object v, Object w) {
    return c.compare(v, m) < 0;
}

private static void exch(Object[] a, int i, int j) {
    Object swap = a[i];
    a[i] = a[j];
    a[j] = swap;
}
1
2
3
4
5
6
7
8
public class Student {
    public static final Comparator<Student> BY_NAME = new ByName();
    ...
    private static class ByName implements Comparator<Student> {
        public int compare(Student v, Student w)
            return v.name.compareTo(w.name);
    }
}

然后可以这样使用排序：

1
Arrays.sort(a, Student.BY_NAME);

使用 Comparator 接口来替代 Comparable 接口的优点就是它支持待排序元素的多种排序规则。

快速排序

快速排序广泛运用于系统排序和其他应用中。它也是一个递归过程，与归并排序不同的是，它先进行操作然后再递归，而不是归并排序先进性递归然后再进行 merge。

算法的思想是先对数组随机打乱，然后每次都把第一个元素放到合适的位置，这个位置左边的元素都比它小，右边的元素都比它大，再将两侧的元素递归操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
private static int partition(Comparable[] a, int lo, int hi) {
    int i = lo, j = hi + 1;
    while (true) {
        while (less(a[++i], a[lo]))
            if (i == hi)
                break;
        while (less(a[lo], a[--j]))
            if (j == lo)
                break;
        if (i >= j)
            break;
        exch(a, i, j);
    }
    exch(a, lo, j);
    return j;
}

public static void sort(Comparable[] a) {
    StdRandom.shuffle(a);
    sort(a, 0, a.length - 1);
}

private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo)
        return;
    int j = partition(a, lo, hi);
    sort(a, lo, j - 1);
    sort(a, j + 1, hi);
}

事实证明，快速排序比归并排序还要快，他最少需要 NlgN 次比较，最多需要 1/2 N^2 次。对于 N 个元素，快速排序平均需要 1.39NlgN 次比较，不过因为不需要过多的元素的移动，所以实际上它更快一些。其中，随机打乱是为了避免最坏的情况。

在空间使用上，它不需要额外的空间，所以是常数级别的。

案例

快速排序的一个案例是找一个数组中第 k 大的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static Comparable select(Comparable[] a, int k) {
    StdRandom.shuffle(a);
    int lo = 0, hi = a.length - 1;
    while (hi > lo) {
        int j = partition(a, lo, hi);
        if (j < k)
            lo = j + 1;
        else if (j > k)
            hi = j - 1;
        else
            return a[k];
    }
    return a[k];
}

这个解法的时间复杂度是线性的，不过有论文表明它的常数很大，所以在实践中效果不是特别好。

多个相同键值

很多时候排序的目的是将相同键值的元素排到一起，处理这种问题不同的排序方法的效率也不同。

归并排序需要 1/2 NlgN 至 NlgN 次比较。

快速排序将达到 N^2 除非 partition 过程停止的键值和结果键值相等，所以需要更好的算法实现.

比较好的一种算法是 Dijkstra 三向切分，它将数组分成了三个部分，是 Dijkstra 的荷兰国旗问题引发的一个思考，即使用三种不同的主键对数组进行排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo)
        return;
    int lt = lo, gt = hi;
    Comparable v = a[lo];
    int i = lo;
    while (i <= gt) {
        int cmp = a[i].compareTo(v);
        if (cmp < 0)
            exch(a, lt++, i++);
        else if (cmp > 0)
            exch(a, i, gt--);
        else
            i++;
    }
    
    sort(a, lo, lt - 1);
    sort(a, gt + 1, hi);
}

对于包含大量重复元素的数组，它将排序时间从线性对数级降低到了线性级别。

系统中的排序

Java 内置了一种排序方法——Arrays.sort()，这个方法使用两种排序方式共同实现。如果排序的是基本数据类型，就使用快速排序；如果排序的是对象，就使用归并排序。

因为对于基本类型来说快速排序会使用更少的空间，而且更快；而归并排序能保证 NlogN 的时间复杂度，而且更加稳定。

在视频的最后，老爷子强调对于不同的应用，要考虑的问题太多了，比如说并行、稳定等等，所以几乎每个重要的系统排序都有一个特定的高效算法，而且目前还有很多算法需要改进。

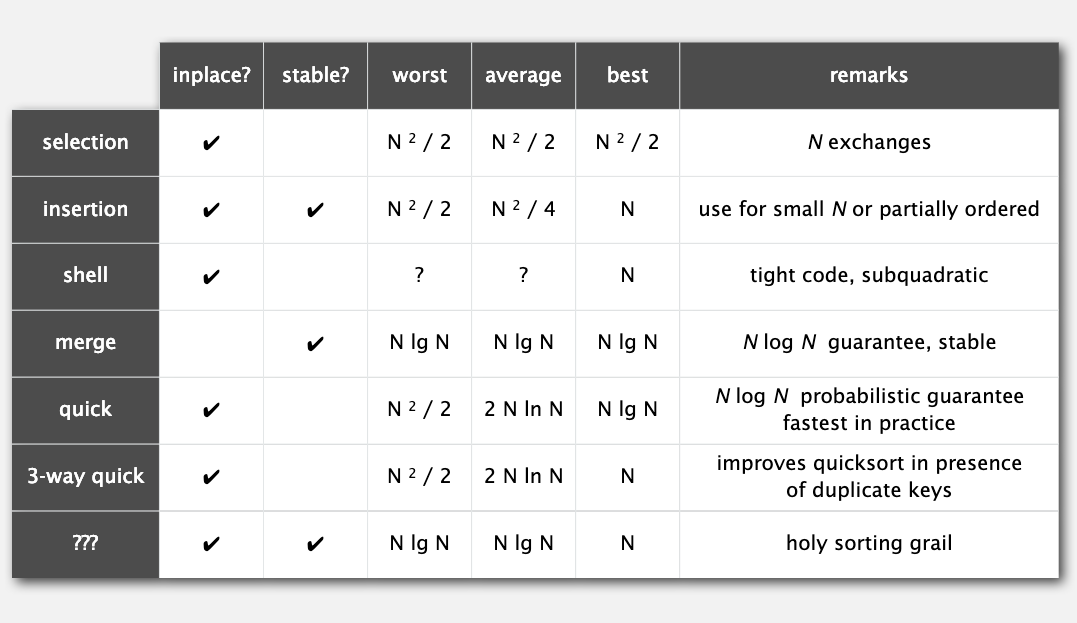
最后附上前面提到过的排序方法的总结：

2

编程作业：模式识别

给 n 个不同的点，找出所连线段，每条线段至少包括四个点。

首先补充完成 Point 类，这部分主要是练习使用 Comparable 和 Comparator 制定排序规则，具体的排序规则文档中有详细的描述。

点击显/隐内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
public class Point implements Comparable<Point> {

    private final int x;     // x-coordinate of this point
    private final int y;     // y-coordinate of this point

    /**
     * Initializes a new point.
     *
     * @param  x the <em>x</em>-coordinate of the point
     * @param  y the <em>y</em>-coordinate of the point
     */
    public Point(int x, int y) {
        /* DO NOT MODIFY */
        this.x = x;
        this.y = y;
    }

    /**
     * Draws this point to standard draw.
     */
    public void draw() {
        /* DO NOT MODIFY */
        StdDraw.point(x, y);
    }

    /**
     * Draws the line segment between this point and the specified point
     * to standard draw.
     *
     * @param that the other point
     */
    public void drawTo(Point that) {
        /* DO NOT MODIFY */
        StdDraw.line(this.x, this.y, that.x, that.y);
    }

    /**
     * Returns the slope between this point and the specified point.
     * Formally, if the two points are (x0, y0) and (x1, y1), then the slope
     * is (y1 - y0) / (x1 - x0). For completeness, the slope is defined to be
     * +0.0 if the line segment connecting the two points is horizontal;
     * Double.POSITIVE_INFINITY if the line segment is vertical;
     * and Double.NEGATIVE_INFINITY if (x0, y0) and (x1, y1) are equal.
     *
     * @param  that the other point
     * @return the slope between this point and the specified point
     */
    public double slopeTo(Point that) {
        /* YOUR CODE HERE */
        if (that == null)
            throw new NoSuchElementException();
        if (this.x == that.x && this.y == that.y)
            return Double.NEGATIVE_INFINITY;
        else if (this.x == that.x)
            return Double.POSITIVE_INFINITY;
        else if (this.y == that.y)
            return +0;
        else
            return (this.y - that.y) * 1.0 / (this.x - that.x);

    }

    /**
     * Compares two points by y-coordinate, breaking ties by x-coordinate.
     * Formally, the invoking point (x0, y0) is less than the argument point
     * (x1, y1) if and only if either y0 < y1 or if y0 = y1 and x0 < x1.
     *
     * @param  that the other point
     * @return the value <tt>0</tt> if this point is equal to the argument
     *         point (x0 = x1 and y0 = y1);
     *         a negative integer if this point is less than the argument
     *         point; and a positive integer if this point is greater than the
     *         argument point
     */
    public int compareTo(Point that) {
        /* YOUR CODE HERE */
        if (that == null)
            throw new NoSuchElementException();
        if (this.x == that.x && this.y == that.y)
            return 0;
        if (this.y < that.y || (this.y == that.y && this.x < that.x))
            return -1;
        return 1;
    }

    /**
     * Compares two points by the slope they make with this point.
     * The slope is defined as in the slopeTo() method.
     *
     * @return the Comparator that defines this ordering on points
     */
    public Comparator<Point> slopeOrder() {
        /* YOUR CODE HERE */
        return new SlopeCompare();
    }

    private class SlopeCompare implements Comparator<Point> {

        @Override
        public int compare(Point o1, Point o2) {
            if (o1 == null || o2 == null)
                throw new NoSuchElementException();
            if (slopeTo(o1) == Double.NEGATIVE_INFINITY && slopeTo(o2) == Double.NEGATIVE_INFINITY)
                return 0;
            else if (slopeTo(o1) == Double.POSITIVE_INFINITY && slopeTo(o2) == Double.POSITIVE_INFINITY)
                return 0;
            else if (slopeTo(o1) == Double.POSITIVE_INFINITY && slopeTo(o2) == Double.NEGATIVE_INFINITY)
                return 1;
            else if (slopeTo(o1) == Double.NEGATIVE_INFINITY && slopeTo(o2) == Double.POSITIVE_INFINITY)
                return -1;
            else if (slopeTo(o1) - slopeTo(o2) > 0)
                return 1;
            else if (slopeTo(o1) - slopeTo(o2) < 0)
                return -1;
                // return slopeTo(o1) - slopeTo(o2) < 0 ? -1 : 1;
            return 0;
        }
    }


    /**
     * Returns a string representation of this point.
     * This method is provide for debugging;
     * your program should not rely on the format of the string representation.
     *
     * @return a string representation of this point
     */
    public String toString() {
        /* DO NOT MODIFY */
        return "(" + x + ", " + y + ")";
    }

    /**
     * Unit tests the Point data type.
     */
    public static void main(String[] args) {
        /* YOUR CODE HERE */
        Point p1 = new Point(0, 10);
        Point p2 = new Point(10, 0);
        System.out.println(p1.slopeTo(p2) == p2.slopeTo(p1));
        Point p3 = new Point(0, 20);
        System.out.println(p3.slopeOrder().compare(p1, p2));
    }
}

然后根据给出的点求所能组成的线段，线段只包含四个点，由两端的点表示，这个方法是暴力方法，4次方的时间复杂度。

点击显/隐内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
public class BruteCollinearPoints {

    /** Record the linesegments */
    private ArrayList<LineSegment> list;

    /**
     * find all line segments containing 4 points
     * @param points
     */
    public BruteCollinearPoints(Point[] points) {
        if (points == null)
            throw new IllegalArgumentException();
        for (Point p : points) {
            if (p == null)
                throw new IllegalArgumentException();
        }
        for (int i = 0; i < points.length - 1; i++) {
            for (int j = i + 1; j < points.length; j++) {
                if (points[i].compareTo(points[j]) == 0)
                    throw new IllegalArgumentException();
            }
        }

        list = new ArrayList<>();
        int N = points.length;
        for (int i = 0; i < N; i++) {
            for (int j = i + 1; j < N; j++) {
                for (int k = j + 1; k < N; k++) {
                    for (int t = k + 1; t < N; t++) {
                        if (points[i].slopeTo(points[j]) == points[i].slopeTo(points[k])
                            && points[i].slopeTo(points[k]) == points[i].slopeTo(points[t]))
                            addLineSegment(points, i, j, k, t);
                    }
                }
            }
        }
    }

    /**
     * Add the line segment to list
     * @param points
     * @param i
     * @param j
     * @param k
     * @param t
     */
    private void addLineSegment(Point[] points, int i, int j, int k, int t) {
        Point[] ps = new Point[]{points[i], points[j], points[k], points[t]};
        Point min = ps[0], max = ps[0];
        for (int index = 1; index < ps.length; index++) {
            if (min.compareTo(ps[index]) > 0)
                min = ps[index];
            if (max.compareTo(ps[index]) < 0)
                max = ps[index];
        }
        list.add(new LineSegment(min, max));
    }

    /**
     * the number of line segments
     * @return
     */
    public int numberOfSegments() {
        return list.size();
    }

    /**
     * the line segments
     * @return
     */
    public LineSegment[] segments() {
        LineSegment[] ans = new LineSegment[list.size()];
        for (int i = 0; i < list.size(); i++) {
            ans[i] = list.get(i);
        }
        return ans;
    }



    public static void main(String[] args) {

    }
}

然后实现高效算法，这里就需要使用前面提到的比较规则，先使用快排将点集排序，取最小的点跟其他点的斜率比，如果达到四个点及以上斜率相同，则记录到数组中。

点击显/隐内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
public class FastCollinearPoints {

    /** Record the linesegments */
    private ArrayList<LineSegment> list;

    /**
     * find all line segments containing 4 or more points
     * @param points
     */
    public FastCollinearPoints(Point[] points) {
        if (points == null)
            throw new IllegalArgumentException();
        for (Point p : points) {
            if (p == null)
                throw new IllegalArgumentException();
        }
        for (int i = 0; i < points.length - 1; i++) {
            for (int j = i + 1; j < points.length; j++) {
                if (points[i].compareTo(points[j]) == 0)
                    throw new IllegalArgumentException();
            }
        }


        list = new ArrayList<>();
        int N = points.length;
        Arrays.sort(points);

        for (int i = 0; i < N - 1; i++) {
            /** get the smallest point */
            Arrays.sort(points);
            Point min = points[i];
            /** sort as the points' slope */
            Arrays.sort(points, i, N, points[i].slopeOrder());

            Point max = null;
            int count = 0;

            for (int j = i + 1; j < N - 1; j++) {
                if (min.slopeTo(points[j]) == min.slopeTo(points[j + 1])) {
                    count++;
                    max = points[j + 1];
                } else if (count != 2) {
                    count = 0;
                }
                if (count >= 2) {
                    count = 0;
                    list.add(new LineSegment(min, max));
                }
            }
        }
    }


    /**
     * the number of line segments
     * @return
     */
    public int numberOfSegments() {
        return list.size();
    }

    /**
     * the line segments
     * @return
     */
    public LineSegment[] segments() {
        LineSegment[] ans = new LineSegment[list.size()];
        for (int i = 0; i < list.size(); i++) {
            ans[i] = list.get(i);
        }
        return ans;
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        int n = in.readInt();
        Point[] points = new Point[n];
        for (int i = 0; i < n; i++) {
            int x = in.readInt();
            int y = in.readInt();
            points[i] = new Point(x, y);
        }

        StdDraw.enableDoubleBuffering();
        StdDraw.setXscale(0, 32768);
        StdDraw.setYscale(0, 32768);
        for (Point p : points) {
            p.draw();
        }
        StdDraw.show();

        FastCollinearPoints collinear = new FastCollinearPoints(points);
        for (LineSegment segment : collinear.segments()) {
            StdOut.println(segment);
            segment.draw();
        }
        StdDraw.show();
    }

}

这次作业目前只拿了88分，应该对于大规模的数据仍有不足。

对了不得不说这门课的 PA 真的有趣：

1

-------------本文结束感谢您的阅读-------------

本文标题:普林斯顿算法课程Part1-week3

文章作者:DianGe Du

发布时间:2019年04月05日 - 09:43

最后更新:2019年06月07日 - 14:40

原始链接:https://dudg1021.github.io/2019/04/05/普林斯顿算法课程Part1-week3.html

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。